티스토리 뷰
프로그래머스 두 원 사이의 정수 쌍 Python
문제
문제 설명
2차원 평면에서 중심이 (0, 0)인 두 개의 원이 주어집니다. 이 두 원의 반지름은 각각 정수 \( r_1 \)과 \( r_2 \)이며, 항상 \( 1 \leq r_1 < r_2 \leq 1,000,000 \)입니다.
두 원 사이의 공간에 존재하는 모든 격자점(즉, \( x \)와 \( y \)가 모두 정수인 점)의 개수를 구하는 문제입니다. 단, 두 원 위에 있는 점들도 포함해서 세야 합니다.
입력
- 정수 \( r_1, r_2 \)
출력
- 조건을 만족하는 격자점 \( (x, y) \)의 개수
테스트케이스
예시 설명 (r1=2, r2=3)
조건은 다음과 같습니다:
\( 2^2 \leq x^2 + y^2 \leq 3^2 \Rightarrow 4 \leq x^2 + y^2 \leq 9 \)
이 조건을 만족하는 \( x, y \in \mathbb{Z} \) 쌍을 모두 찾아 개수를 세면 결과는 20입니다.
문제 작동원리
- 원의 방정식은 다음과 같습니다:
- 내부 원: \( x^2 + y^2 = r_1^2 \)
- 외부 원: \( x^2 + y^2 = r_2^2 \)
- 우리가 찾는 점들은 다음 조건을 만족해야 합니다:
\( r_1^2 \leq x^2 + y^2 \leq r_2^2 \)
- 이 점들은 격자점이므로 \( x, y \)는 모두 정수입니다.
- (0, 0)을 중심으로 하여 대칭적인 모양을 가지고 있으므로, 1사분면(양의 \( x, y \))만 구한 후 4를 곱하면 전체 개수를 구할 수 있습니다.
- 단, \( x = 0 \) 축에 해당하는 경우는 따로 고려할 필요 없이 자동 보정됩니다. \( x=0 \)은 루프에서 제외되고, \( y=0 \) 축이 과대 계산되므로 이 둘이 정확히 상쇄됩니다.
아이디어
핵심 아이디어 요약
- 대칭성 활용
전체 평면의 정수 쌍을 세기보다, 한 쪽 사분면만 계산해서 ×4로 처리하면 계산량이 크게 줄어듭니다. - 각 \( x \)에 대해 가능한 \( y \) 범위를 구함
\( r_1^2 \leq x^2 + y^2 \leq r_2^2 \Rightarrow \sqrt{r_1^2 - x^2} \leq y \leq \sqrt{r_2^2 - x^2} \)
단, \( y \)가 정수이므로:- 최소 \( y \): \( \lceil \sqrt{\max(0, r_1^2 - x^2)} \rceil \)
- 최대 \( y \): \( \lfloor \sqrt{r_2^2 - x^2} \rfloor \)
- 가능한 \( y \) 개수 세기
\( y_{\text{개수}} = y_{\max} - y_{\min} + 1 \)
- 전체 개수는 \( x>0 \) 범위에서 위 개수를 모두 더한 후 ×4
아이디어 진행과정
중심이 원점인 두 원: 원의 방정식
중심이 원점 \( (0, 0) \)이고, 반지름이 \( r \)인 원의 방정식은 다음과 같습니다.
\( x^2 + y^2 = r^2 \)
이 방정식을 기준으로:
- 원의 내부 또는 원 위의 점은
\( x^2 + y^2 \leq r^2 \)
- 원의 외부 또는 원 위의 점은
\( x^2 + y^2 \geq r^2 \)
이 성질을 이용해서, 두 원 사이의 공간에 있는 점은 다음 두 가지 조건을 동시에 만족해야 합니다:
- 작은 원 \( r_1 \)의 바깥쪽이거나 위
- 큰 원 \( r_2 \)의 안쪽이거나 위
예시 설정: \( r_1 = 2 \), \( r_2 = 3 \), \( x = 1 \)
두 원의 반지름을 고정합니다.
\( r_1 = 2, \quad r_2 = 3 \)
특정 x값, 즉 \( x = 1 \)로 고정했을 때, 그에 따라 가능한 \( y \)의 정수값을 찾아보는 것이 목표입니다.
조건 ①: 작은 원 바깥 (또는 위) — 내부 원의 조건
\( x^2 + y^2 \geq r_1^2 \Rightarrow x^2 + y^2 \geq 4 \)
1단계: x값을 대입
x가 1이므로 \( x^2 = 1 \)입니다.
위 식에 대입하면 다음과 같습니다:
\( 1 + y^2 \geq 4 \)
2단계: 식을 정리해서 y에 대해 풀기
\( y^2 \geq 3 \)
즉, y제곱이 3보다 크거나 같아야 합니다.
3단계: 절댓값 부등식으로 바꾸기
\( y^2 \geq 3 \)이므로, \( y \)의 절댓값은 반드시 \( \sqrt{3} \) 이상이어야 합니다.
\( |y| \geq \sqrt{3} \)
4단계: \( \sqrt{3} \)이 어떤 정수 사이에 있는지 비교
\( \sqrt{3} \)이 어떤 값보다 크고 어떤 값보다 작은지를 파악하기 위해, 정수의 제곱으로 비교합니다.
다음처럼 확인할 수 있습니다:
\( 1^2 = 1 < 3 < 4 = 2^2 \Rightarrow 1 < \sqrt{3} < 2 \)
즉, \( \sqrt{3} \)은 약 1.732이므로, 절댓값이 이보다 크거나 같은 정수는 2 이상이라는 뜻입니다.
결과: 조건 ①을 만족하려면
\( |y| \geq \sqrt{3} \Rightarrow |y| \geq 2 \)
가능한 정수 y는
\( y = \pm 2, \pm 3, \pm 4, \dots \)
조건 ②: 큰 원 안쪽 (또는 위) — 외부 원의 조건
\( x^2 + y^2 \leq r_2^2 \Rightarrow x^2 + y^2 \leq 9 \)
1단계: x값을 대입
\( x = 1 \Rightarrow x^2 = 1 \)
식에 대입하면:
\( 1 + y^2 \leq 9 \)
2단계: 식을 정리해서 y에 대해 풀기
\( y^2 \leq 8 \)
3단계: 절댓값 부등식으로 바꾸기
\( y^2 \leq 8 \Rightarrow |y| \leq \sqrt{8} \)
4단계: \( \sqrt{8} \)이 어떤 정수 사이에 있는지 비교
\( 2^2 = 4 < 8 < 9 = 3^2 \Rightarrow 2 < \sqrt{8} < 3 \)
즉, \( \sqrt{8} \approx 2.828 \)
절댓값이 이보다 작거나 같은 정수는 2 이하입니다.
결과: 조건 ②를 만족하려면
\( |y| \leq \sqrt{8} \Rightarrow |y| \leq 2 \)
가능한 정수 y는
\( y = -2, -1, 0, 1, 2 \)
두 조건을 동시에 만족하는 y는?
- 조건 ①: \( |y| \geq 2 \Rightarrow y = -2, 2, 3, -3, \dots \)
- 조건 ②: \( |y| \leq 2 \Rightarrow y = -2, -1, 0, 1, 2 \)
두 조건을 동시에 만족하려면,
절댓값이 2 이상이면서도 2 이하여야 하므로,
\( |y| = 2 \Rightarrow y = -2, 2 \)
\( r_1 = 2, r_2 = 3 \)인 경우
x = 2, x = 3일 때 가능한 정수 y 값 찾기
x = 2일 때
조건 ①: 내부 원 바깥 (또는 위)
\( x^2 + y^2 \geq r_1^2 = 4 \)
1. x = 2이므로
\( x^2 = 4 \)
2. 식에 대입하면
\( 4 + y^2 \geq 4 \Rightarrow y^2 \geq 0 \)
3. 이 부등식은 항상 참입니다. 어떤 y값이든지 \( y^2 \geq 0 \)이므로, 모든 y에 대해 이 조건은 만족합니다.
→ 조건 ①은 x = 2일 때 항상 만족합니다.
조건 ②: 외부 원 안쪽 (또는 위)
\( x^2 + y^2 \leq r_2^2 = 9 \)
1. x = 2이므로
\( x^2 = 4 \)
2. 식에 대입하면
\( 4 + y^2 \leq 9 \Rightarrow y^2 \leq 5 \)
3. 절댓값 부등식으로 정리하면
\( |y| \leq \sqrt{5} \)
4. \( \sqrt{5} \)는 어떤 두 정수 사이에 있는가?
\( 2^2 = 4 < 5 < 9 = 3^2 \Rightarrow 2 < \sqrt{5} < 3 \Rightarrow |y| \leq \sqrt{5} \Rightarrow |y| \leq 2 \)
5. 정수 y의 가능한 값:
\( y = -2, -1, 0, 1, 2 \)
→ 조건 ②를 만족하는 y는 총 5개
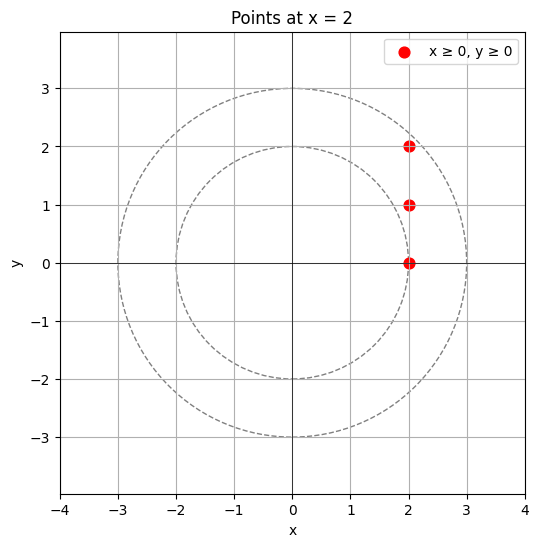
x = 2일 때 최종 y 정수 값:
조건 ①: 항상 만족 (모든 y 가능)
조건 ②: \( y = -2, -1, 0, 1, 2 \)
∴ 동시에 만족하는 y는
\( y = -2, -1, 0, 1, 2 \)
x = 3일 때
조건 ①: 내부 원 바깥 (또는 위)
\( x^2 + y^2 \geq r_1^2 = 4 \)
1. x = 3이므로
\( x^2 = 9 \)
2. 대입하면
\( 9 + y^2 \geq 4 \Rightarrow y^2 \geq -5 \)
3. \( y^2 \geq -5 \)는 항상 참입니다. 어떤 y도 이 조건을 만족합니다.
→ 조건 ①은 x = 3일 때 항상 만족.
조건 ②: 외부 원 안쪽 (또는 위)
\( x^2 + y^2 \leq r_2^2 = 9 \)
1. x = 3이므로
\( x^2 = 9 \)
2. 대입하면
\( 9 + y^2 \leq 9 \Rightarrow y^2 \leq 0 \)
3. y^2 ≤ 0이기 때문에, 오직 \( y^2 = 0 \)만 가능합니다.
4. \( y^2 = 0 \Rightarrow y = 0 \)
→ 조건 ②를 만족하는 y는 단 하나:
\( y = 0 \)
x = 3일 때 최종 y 정수 값:
조건 ①: 항상 만족
조건 ②: \( y = 0 \)
∴ 가능한 y는 오직
\( y = 0 \)

정리표: 각 x값에서 가능한 y 정수들
최종 결론: x = 1일 때 가능한 y 정수
조건을 모두 만족하는 y는 오직 \( y = 2 \), \( y = -2 \) 단 두 개입니다.
이 중에서 파이썬 코드에서는 \( y \geq 0 \)만 먼저 구하고, 나중에 4사분면 대칭을 곱하기 때문에, y = 2만 한 번 계산되며, 전체 카운트에는 4배가 반영됩니다.
전체코드
import math
def solution(r1, r2):
answer = 0
for x in range(1, r2 + 1):
# r1보다 큰 y값 중 가장 작은 정수
y_min = math.ceil(math.sqrt(max(0, r1**2 - x**2)))
# r2보다 작거나 같은 y값 중 가장 큰 정수
y_max = math.floor(math.sqrt(r2**2 - x**2))
if y_max >= y_min:
# 해당 x에서 가능한 y 개수 × 4 (대칭)
answer += (y_max - y_min + 1) * 4
return answer
결론
- 이 문제는 수학적 해석과 계산 최적화를 동시에 요구합니다.
- 중심이 원점이고, 대칭 구조를 가지고 있기 때문에 대칭을 활용하여 계산량을 줄이는 것이 핵심입니다.
- 핵심 연산은 각 \( x \) 좌표에 대해 가능한 \( y \)의 범위를 제곱근 함수와 올림/내림 함수로 계산하여, 격자점의 개수를 빠르게 구하는 방식입니다.
- 축에 있는 점들의 과소/과대 계산 문제는 코드에서 자동으로 상쇄되므로 별도 처리 없이 정확한 결과를 얻을 수 있습니다.
- 시간복잡도는 \( O(r_2) \)이며, 최대 \( 10^6 \)까지 무리 없이 동작합니다.
'백준 스터디 > 프로그래머스' 카테고리의 다른 글
| 프로그래머스 뒤에 있는 큰 수 찾기 python (0) | 2025.09.15 |
|---|---|
| 프로그래머스 요격 시스템 Python (0) | 2025.09.14 |
| 프로그래머스 연속된 부분 수열의 합 python (0) | 2025.09.14 |
| 프로그래머스: 과제 진행하기 (Python) (0) | 2025.09.12 |
| 프로그래머스 광물 캐기 Python (0) | 2025.09.09 |
- Total
- Today
- Yesterday
- 알고리즘문제풀이
- 동적 계획법
- c언어
- C++
- 브루트포스
- 백준
- 코딩테스트
- python 알고리즘
- 동적계획법
- 그리디알고리즘
- 코딩
- HTML
- 코딩 테스트
- 알고리즘
- Python
- 프로그래머스
- dfs
- DP
- 문제 풀이
- 프로그래밍
- 알고리즘 문제풀이
- 파이썬코딩
- 문제풀이
- 파이썬
- 그리디
- 문자열처리
- 객체지향
- 그래프 탐색
- 알고리즘기초
- 상속
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |

